光栅化

三角形的光栅化

光栅化是将几何图形（如三角形等多边形）转化拆分为屏幕上像素网格并着色的过程。是将连续空间转化为离散像素空间的关键步骤。

对于每个像素，要决定它是否被图形覆盖，并计算颜色值写入帧缓冲。

像素是屏幕上的最小单位，用RGB三个值表示颜色。

从模型空间到屏幕空间的变换流程

(1) MVP变换（Model-View-Projection）

• 变换顺序为：模型空间 → 世界空间 → 相机空间 → 裁剪空间（clip space）。
• 最后将得到裁剪空间坐标（Clip Space），其坐标范围为齐次坐标系中[−w, w]的立方体。

(2) 齐次除法

• 将裁剪空间坐标除以w分量，得到归一化设备坐标（NDC, Normalized Device Coordinates）。
• NDC坐标范围为[−1, 1]³，即一个单位立方体。

(3) 视口变换（Viewport Transform）

• 将NDC映射到屏幕空间（screen space）：[0, width] × [0, height]。
• 映射公式：

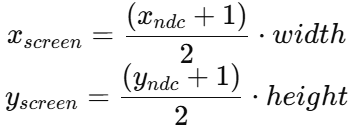
• Z轴可线性缩放为[0,1]区间，用于深度测试。

帧缓冲区（Frame Buffer）

定义：屏幕上的图像数据将被存储在一块内存区域中，称为帧缓冲区。

每个像素存储颜色值（RGB或RGBA）和深度值（用于Z-buffer）。

光栅化流程：以三角形为例

输入：已经过MVP和视口变换的屏幕空间三角形。

目标：确定哪些像素属于该三角形，计算它们的颜色并写入帧缓冲。

为什么选择三角形？三角形为何是图形学中的基本图元？

• 任意多边形都可以被分解为三角形（通过三角剖分）。
• 三角形一定是平面图形，不会出现非平面情况。
• 内部定义明确，插值容易实现（后面会讲 barycentric interpolation）。

如何判断一个像素是否在三角形内部？

可以采用方法：逐像素采样 + Inside Test

1. 遍历所有像素的中心（例如 (x + 0.5, y + 0.5)），对屏幕空间进行采样。
2. 对于每个像素中心，调用 inside() 函数判断是否在三角形内部。

如何判断像素中心是否在三角形内？insider()函数的核心算法逻辑为：

• 假设三角形为 ABC，像素中心为 P。
• 构造三个向量叉乘：AB×AP,BC×BP,CA×CP。
• 如果三个叉积在Z轴方向上符号一致，说明点P在三角形内部（右手定则）。

优化：Bounding Box（包围盒）（P43）

• 由于遍历全屏像素代价太高，所以可以使用该方法。
• 计算三角形的包围盒，使用最小外接矩形来限定像素遍历范围，提高效率。
• 可用 min/max(x1,x2,x3) 来限定包围盒x和y的范围。
• 然后只需遍历 (x, y) ∈ bounding box 中的像素，做 inside 判断。

————————————————————————————————————————

MVP变换 -> 视口变换 = 将(1 ~1)³的空间映射到屏幕空间。当所有三角形都到屏幕上后，就把东西画在屏幕上（光栅化）。

P11: 视口变换矩阵，Z为1暂时不变

把-1 ~ 1三次方的正方体放到屏幕上

抗锯齿和反走样anti-Aliasing

什么是走样？

走样是指由于采样不充分或采样方式不合理，导致图像出现“锯齿状边缘”、“闪烁”、“波纹”等视觉伪影。

走样的三种典型表现（P18）：

1. Jaggies（锯齿）：边缘不平滑，出现锯齿效果。
2. Moire Patterns（摩尔纹）：细节图案在屏幕上呈现奇怪的干涉图案。
3. Temporal Aliasing（时间走样）：动画播放中出现闪烁或跳变现象。

为什么会发生走样？

• 函数（图像）的变化频率太高，而采样率不够，导致信号不能正确还原（违反了奈奎斯特定理）。

从频域与傅里叶变换的视角看待走样

时域 vs 频域：

• 时域：从空间/时间角度看信号。
• 频域：从“频率”角度看信号的组成。

▶ 傅里叶级数与傅里叶变换（P30~P35）：

• 傅里叶级数：任何周期函数都可以表示为一组正弦/余弦函数的线性组合。
• 傅里叶变换：将任意函数映射到频率空间，揭示其频率组成。

▶ 高频 = 细节、边缘，低频 = 平坦、模糊区域

走样的频域解释（P50-P51）

▶ 采样过程 = 时域乘积，对应频域卷积。

• 采样会在频域上造成信号频谱的“重复（复制粘贴）”。
• 如果原始信号中存在高频成分，这些高频会与复制频谱发生“混叠”（Overlapping），造成走样。

反走样（Anti-Aliasing）的方法

方法一：提高采样率（Supersampling）

原理：

通过在每个像素内使用更多的采样点（例如 4x, 8x）来更准确评估图形是否覆盖该像素。

示例：MSAA（Multi-Sample Anti-Aliasing）

• 对每个像素划分多个子像素采样点。
• 判断每个采样点是否在图形内部（被三角形覆盖）。
• 最终颜色 = 所有采样点颜色的平均值。

方法二：先模糊再采样（Filtering Before Sampling）

核心思想：

在采样前，先对图像进行模糊处理（低通滤波），把高频成分滤除，从而避免混叠。

原理：

低通滤波 + 采样 = 保留低频部分 → 减少走样。

如何模糊一个三角形？

• 使用一个一定大小的滤波核（Kernel），对图形进行卷积。
• 本质上是取一个像素周围的邻域，做加权平均（Blur）。

卷积与滤波（P41~P45）：

• 卷积操作 = 用滤波器函数在图像上滑动、叠加。
• 时域卷积 = 频域乘积。

其他反走样方法（现代渲染中常用）

▶ 1. FXAA（Fast Approximate Anti-Aliasing）

• 基于图像后处理（屏幕空间）。
• 对检测到锯齿边缘的区域进行模糊滤波。
• 优点：快速、便宜，适合游戏。
• 缺点：不是物理真实，不影响几何覆盖，只是图像平滑处理。

▶ 2. TAA（Temporal Anti-Aliasing）

• 结合多个时间帧之间的采样信息。
• 通过当前帧和上一帧的像素结果融合来抑制锯齿。
• 优点：性能和质量兼顾，适合动态场景。
• 缺点：可能出现鬼影、模糊，需要motion vector矫正。

总结：

┌──────────────────────┐
│   光栅化 = 采样过程   │
└─────────┬────────────┘
          ▼
   ┌────────────┐
   │   走样 Aliasing  │
   └────┬─────────┘
        │
        ├─ 锯齿 / 闪烁 / 摩尔纹
        ├─ 原因：采样频率 < 信号频率
        └─ 频域角度：混叠（aliasing）

解决方案：反走样（Anti-Aliasing）
├─ 方法1：提高采样率
│   └─ MSAA（Multi-Sample Anti-Aliasing）
├─ 方法2：先模糊再采样
│   └─ 滤波（低通）+ 卷积
├─ 后处理：图像级别
│   ├─ FXAA：快速近似抗锯齿（图像模糊）
│   └─ TAA：时间抗锯齿（帧间融合）

————————————————————————————————————————

光栅化的过程：在屏幕空间内，用一系列离散的点（即像素的中心）对是否在三角形内进行函数的采样。

视频：在时间中进行采样

采样会造成：Sampling Artifacts，即瑕疵/错误

它有三种类型：P18

造成这种现象的原因：信号变化太快，以至于采样跟不上它的速度。

Frequency Domain频域

(1)P29频率：正弦波余弦波的频率

P30傅里叶级数展开：任何一个周期函数，都可以把它写成一系列正弦函数和余弦函数的线性组合与常数项的和。

P31傅里叶变换：本质上是把函数变成不同频率的段，然后把它们显示出来。

P35傅里叶变换的作用：从时域变换到频域。可以让人看到，一个图像在不同的频率长什么样。

P32举个例子：函数本身的频率和采样的频率之间的关系。

P33走样定义：同样的采样方法，去采样两种不同频率的函数，得出的结果无法区分。

那么如何进行反走样？

P21在采样前，先进行模糊滤波（filtering），然后采样这个模糊的图形。

顺序反过来不行！因为先做采样再做模糊，

滤波：把某一些特定的频率抹掉，看看对应的信号会如何变换。

P26高通滤波可以看出什么是边界：颜色之间变化很大，即认为是高频信息。

P27低通滤波

滤波 = 平均（模糊） = 卷积（把三角形任何一个点，取周围的一块）

P41卷积：作用在一个信号上，利用某一种滤波器，对它进行卷积，从而得到一个新的信号。

P45时域的卷积 = 频域的乘积

P47-P48：越大的盒子，越模糊

什么是采样？重复这个频域上的内容

P50时域上的乘积 = 频域上的卷积

P51采样就是重复一个原始信号的频谱。因此可以知道，走样就是因为采样不同的间隔，会引起频谱以另外不同的间隔移动。从频率的角度看，频谱在经过复制粘贴后，出现了混合，因此造成了走样。

反走样

P53方法1：增加采样率

方法2：先做模糊，即低通滤波，把高频信息拿掉，然后再采样。

为什么这种方法可以呢？P54

那么怎么才能把一个三角形变模糊呢？

用一个一定大小的低通滤波器对它进行卷积。P58

一种抗锯齿方式：MSAA是什么？实际上对信号进行模糊的操作

P62 – P67把一个像素划分成一些小的像素（增加采样点），从而得到一个准确的近似。本质上是增加采样点，而不是提高分辨率。

其他方法：FXAA和TAA